Most students would tell you that Geometry and Algebra are two completely separate subjects, which is wrong. We can use algebra to make sense of geometry and we can use geometry to help make sense of algebra. I know, it sounds crazy, but it is true. One main concept among algebra and geometry is patterns. Students can use graphs or tables to view the patterns among shapes dimensions and other values such as area, perimeter or surface area.
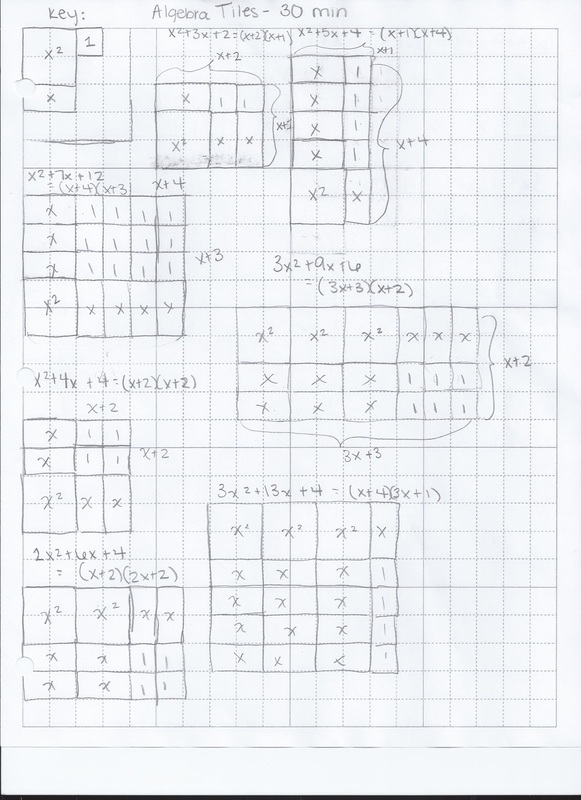
One example is using squares and rectangles to factor an equation. Here is a link to problems with the option of different levels of difficulty to factor an equation using the knowledge of area of squares and rectangles being length times width to find what a polynomial factors into. We use the units of length multiplied by the units of height to find the two factors. Similarly, We can use our knowledge of area and/or patterns when looking at certain patterns to find an algebraic equation. Here is an example:
One example is using squares and rectangles to factor an equation. Here is a link to problems with the option of different levels of difficulty to factor an equation using the knowledge of area of squares and rectangles being length times width to find what a polynomial factors into. We use the units of length multiplied by the units of height to find the two factors. Similarly, We can use our knowledge of area and/or patterns when looking at certain patterns to find an algebraic equation. Here is an example:
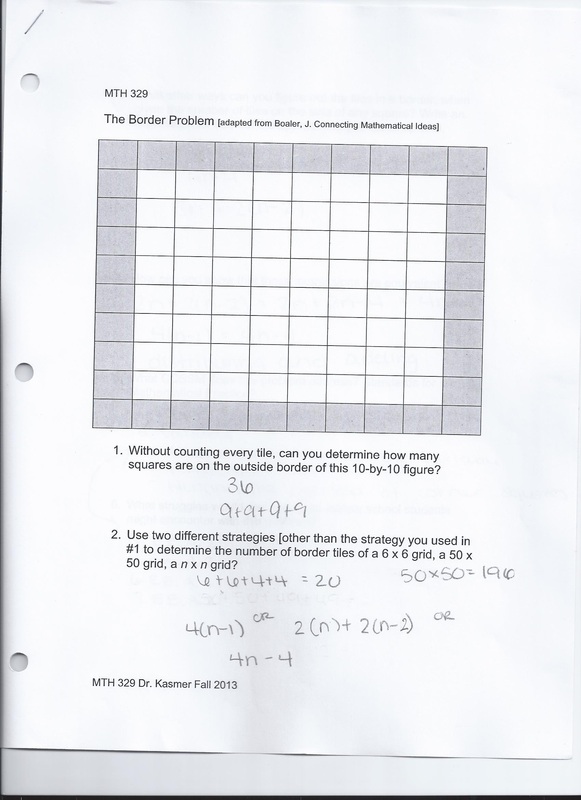
Next, we can look at the perimeter among the different dimensions of shapes. We can use the pattern of the values to find an equation that will allow us to find any perimeter based on dimension or find the dimension based on the perimeter. I saw an activity in a 8th grade classroom where students used toothpicks to find the perimeter of one hexagon. Then, connected another hexagon to one side of the previous hexagon, then counted the perimeter of the figure created from both hexagons and how many total, and found a pattern creating an algebraic expression that allowed them to find the amount of toothpicks that would be needed for 10 hexagons and how many toothpicks would be needed for the perimeter. Another activity was finding the perimeter of different sized squares based on looking at one square. This example is posted below.
Another way that geometry has been connected to algebra is the equation of the volume of a cone and a sphere compared to a cylinder. In one of my previous math classes, I had an assignment to teach a lesson that demonstrated why the area of a cone is one third pi times r squared times height and the volume of a sphere is four thirds pi times r cubed. We constructed a cylinder with transparent plastic and a sphere with playdough such that they both have the same height and circumference. The students then smash the plateau inside of the cylinder and are able to notice the sphere's volume takes about two thirds of the cylinder, allowing students to make the connection between the volume of the cylinder and the sphere to be two thirds. We then must see if there were any other generalizations we could make with the height, which students realize the height of the sphere is 2r, giving us the equation we are looking for. This visual geometric representation allows students to make the algebraic formula for the volumes. For the cone, students create a cone with same circumference at the base of the cone as the cylinder and contains the same height using construction paper, then fill it with rice and dump it in the cylinder and notice it takes up one third of the cylinder, giving us the equation of a cone to be one third pi r squared times height.
These are just three of many more relationships among algebra and geometry. In a way, geometry is just a visual representation of the algebra. It has been proven that using visuals and discovery based activities students are able to learn more conceptually instead of a procedural approach which is more beneficial for the students. Realizing the connection among geometry and algebra is beneficial for everyone!
These are just three of many more relationships among algebra and geometry. In a way, geometry is just a visual representation of the algebra. It has been proven that using visuals and discovery based activities students are able to learn more conceptually instead of a procedural approach which is more beneficial for the students. Realizing the connection among geometry and algebra is beneficial for everyone!
 RSS Feed
RSS Feed
